Home
/
Blogs
/
Mojo Performance Analysis

Mojo Performance Analysis

Published: April 29, 2025

Abstract:

This study evaluates the performance of matrix multiplication and linear regression implementations in Mojo and Python, using both naive and optimized approaches. The experiment was conducted on two distinct environments: a local Apple M4 Pro chip-powered system and a Modular MAX container deployed in its default mode without resource constraints.

Reason for this Analysis:

Evaluating new technologies like Mojo helps us explore new opportunities to accelerate our ML infrastructure and internal tooling. This performance analysis helps assess whether Mojo could complement or replace existing components in our data processing stack, especially when execution speed and resource efficiency are key.

By comparing Mojo’s real-world performance against Python, we aim to understand its maturity, practical benefits, and potential fit within Pvotal’s Infrastream ecosystem, particularly for ML workflows, model refinement pipelines, and customer-facing products that demand scalable computation.

Introduction:

Mojo, a new superset of Python designed for high-performance computing, aims to bridge this gap by combining Python's ease of use with the performance benefits traditionally associated with lower-level languages. This study investigates Mojo's potential by comparing its performance to Python implementations across naive and optimized versions of matrix multiplication and linear regression.

Linear Regression:

Linear regression[11] is a fundamental statistical and machine learning technique used to model the relationship between a dependent variable and one or more independent variables. It assumes a linear relationship between the inputs and the output.

The linear regression equation is as follows,

Where,

ŷ is the predicted output vector
X is the input matrix
w is the weight vector
b is the bias term (scalar)

Linear regression serves as a building block for more complex machine learning models and is widely used in various fields for prediction and analysis.

Naive vs Optimised Matrix Multiplication:

Matrix multiplication is a fundamental operation in linear algebra that combines two matrices to produce a new matrix. In the context of linear regression, matrix multiplication is used to efficiently compute predictions for multiple data points simultaneously.

The gradient calculation in linear regression involves matrix multiplication to efficiently compute the partial derivatives of the loss function with respect to the model parameters. Specifically, the gradient of the weights is calculated as

Where,

X^T transpose of the input matrix X
ŷ is the predicted output vector
y is the true output vector
w is the weight vector

This matrix multiplication allows for simultaneous computation of gradients across all weights, making the process more efficient for large datasets. The gradient is crucial for updating the model parameters during training, guiding the training process towards the minimum of the loss function.

The time complexity of naive matrix multiplication is O(n³) for square matrices of size n * n.

This is because:

For each element in the result matrix (n² elements)
We perform n multiplications and n - 1 additions

For non-square matrices, the complexity is O(n * m * p) where m, n, and p are the dimensions of the matrices being multiplied.

Example of how complexity scales:

n	Operations (n³)	Time(Assuming 1 ns per operation)
100	1,000,000	1 ms
1000	1,000,000,000	1 s
10000	1,000,000,000,000	1000 s / 16.67 minutes

The time complexity scales rapidly with increasing matrix size. This is why optimized algorithms, vectorization and multithreading are crucial for efficient matrix operations in practice.

Experimental Setup:

1. Implementations
Four implementations were tested:

Mojo Naive: A sequential implementation using three nested loops for matrix multiplication.
Mojo Optimized: An optimized implementation leveraging Mojo's parallelization (multi-threading) and vectorization (SIMD[10]).
Python Naive: A basic Python implementation using sequential loops similar to Mojo Naive.
Python Optimized (NumPy[12]): An implementation utilizing NumPy's highly optimized matrix operations.

2. Platforms

Apple M4 Chip[13]:
- Hardware: 12-core CPU with 8 performance cores and 4 efficiency cores 16-core GPU, 16-core Neural Engine.
- Memory: 24GB unified memory with 273GB/s bandwidth.
Modular Max Container[3][7]:
- Runtime Environment: Modular MAX container running in its default configuration with no resource constraints.

3. Dataset Generation
To ensure consistency across all tests, a dataset was generated using the following parameters:

Matrix X: m × n dimensions (m=1024, n=512)
Target vector y: m × k dimensions (m=1024, k=1)

4. Performance metrics:
The following metrics were recorded for each implementation:

Execution Time(s): Measured from the start to the completion of matrix multiplication and linear regression. The unit used here is seconds.
Mean Squared Error (MSE)[4]: MSE measures the amount of error in predictions. It assesses the average squared difference between the observed and predicted values.

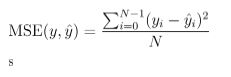
Where,

y refers to the true value
ŷ refers to the predicted value
And N refers to the total number of samples

Results:

1. Performance comparison table

Environment	Implementation	Mojo’s Time (s)	Python’s Time (s)	Mojo’s Loss (MSE)	Python’s Loss (MSE)
Local Machine	Optimized	1.273788	0.092018	0.054588	0.038764
Local Machine	Not Optimized	2.448100	65.743995	0.041605	0.039917
MAX Container	Optimized	3.107345	0.108693	0.058131	0.039215
MAX Container	Not Optimized	2.740271	82.625032	0.041605	0.039404

Where,

s refers to seconds (unit of time)
MSE refers to Mean Squared Error (Metric used to calculate loss)

2. Key Observations:

(a) Execution Time:

On the local machine (Apple M4 Pro), optimized Python (NumPy) outperforms all other implementations.
Mojo shows consistent performance between optimized and non-optimized versions on the local machine.
In Local machine, optimized Mojo script outperforms non-optimized script.
In the Max container, non-optimized Mojo script slightly outperforms optimized script.
Python's non-optimized version is significantly slower than all other implementations.

(b) Loss Values

All implementations converge[14] to similar loss values, indicating consistency in the results.
Mojo implementations show identical loss values for optimized and non-optimized versions in both environments.
Python implementations show slight variations in loss between optimized and non-optimized versions due to the numpy random initialization

The MAX container environment shows increased execution times compared to the local machine for all implementations. But relatively, mojo non-optimized has minimal increase in execution time.

Conclusion:

For Python, the huge gap between optimized and non-optimized versions justifies the effort of using optimized libraries or writing optimized code.
For Mojo, the consistent performance suggests that we can even achieve good performance without extensive optimization.
For Pvotal, the results of this analysis confirm our decision to adopt Mojo. Its predictable performance, seamless hardware abstraction, and developer-friendly syntax make it a powerful addition to our toolkit. We're already in the process of integrating it with Infrastream to streamline our development workflow further.
Looking ahead, the potential of the Modular-MAX engine[15] seems very interesting. By reducing our dependence on Nvidia GPUs, we could significantly lower infrastructure costs while maintaining high performance. This aligns with our long-term strategy of building scalable, cost-efficient systems without compromising capability.

Author: Jeffrey J Sam
Machine Learning Engineer at Pvotal, focused on computer vision and large vision-language models, with experience collaborating on AI projects with NASA.

Co-Author: Ashley Manraj
Chief Technology Officer at Pvotal and a veteran security expert with over a decade of experience in open-source innovation.

References:

Mojo Performance Analysis

Table of Contents

Abstract:

Reason for this Analysis:

Introduction:

Linear Regression:

Naive vs Optimised Matrix Multiplication:

Experimental Setup:

Results:

Conclusion: